直方图最大矩形(单调栈)

发表于 | 更新于 | 分类于

经典版

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图，矩形的宽度都为1：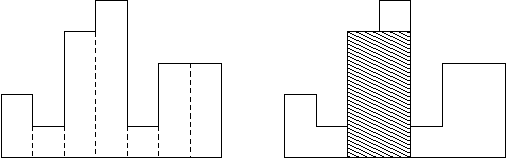
1.gif
通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式

输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数n开始，表示组成直方图的矩形数目。

然后跟随n个整数h1，…，hn。

这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为1。

同行数字用空格隔开。

当输入用例为n=0时，结束输入，且该用例不用考虑。

输出格式

对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围

1≤n≤100000,
0≤hi≤1000000000

输入样例：

1
2
3
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出样例：

1
2
8
4000

方法一

yxc老师做法
对于每一个矩形，去找左右两边能扩展到的最远边界，那么问题就转化为了
找两次边界，而单调栈就是找到第一个比它小的元素，栈里存放下标
栈内要满足单调性

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 100005;
int a[N], l[N], r[N], s[N], n;		//初始数组，左右边界，数组模拟栈，数据个数
typedef long long ll;		//乘积可能爆long long
void one_side(int b[])
{
    int top = 1;		//栈顶指针
    a[0] = -1;		//哨兵元素，当s[top] == 0时，即前面所有元素比当前要入栈的a[i]大
			//此时a[0] == -1 < a[i](最小为0)，处理掉了边界情况b[i] = 1, wid = 1 - 1 + 1 = 1
    for(int i = 1; i <= n; i ++ )		
    {
        while(a[s[top]] >= a[i])		//删除栈中比a[i]大的元素，保持单调性
            top --;
        b[i] = s[top] + 1;		//边界为栈顶 + 1
        s[++ top] = i;	//新元素入栈			
    }
}

int main()
{
    while(cin >> n, n)
    {
        for(int i = 1; i <= n; i ++ )
            scanf("%d", &a[i]);
        one_side(l);			//找左边界
        reverse(a + 1, a + n + 1);		//转置找右边界
        one_side(r);		
        ll ans = 0;
        for(int i = 1, j = n ; i <= n; i ++ , j -- )		//左右对应下标运算
            ans = max(ans, (ll)a[i] * (n - l[j] + 1 - r[i] + 1));	//都转化为离终点的距离
        cout << ans << endl;
    }
    return 0;
}

方法二

lyd做法

思想

运用单调栈维护每个元素的左边界，利用w[]数组记录每个元素的向右延伸的宽度
利用哨兵元素a[n + 1] == 0清空栈内剩余元素，对于每一次出栈，实时更新
栈顶元素的值 * 向右延伸最远宽度(width)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 100005;
int a[N], w[N], s[N];
int main()
{
    int n, top = 0;
    while(cin >> n, n)
    {
        for(int i = 1; i <= n; i ++ )
            scanf("%d", &a[i]);
        a[n + 1] = 0, top = 0;
        ll ans = 0;
        for(int i = 1; i <= n + 1; i ++ )
        {
            if(a[i] > s[top])			//大于栈顶直接入栈，左宽度为1
                s[++ top] = a[i], w[top] = 1;
            else
            {
                int width = 0;	
                while(a[i] < s[top])		//出栈顶元素的时候实时更新
                {
                    width += w[top];
                    ans = max(ans, (ll)width * s[top]);
                    top --;
                }
                s[++ top] = a[i], w[top] = width + 1;		
						//删完后入栈，前面元素的最远宽度加上本身1作为左宽度
            }
        }
        cout << ans << endl;
    }
    return 0;
}

扩展(城市游戏)

有一天，小猫rainbow和freda来到了湘西张家界的天门山玉蟾宫，玉蟾宫宫主蓝兔盛情地款待了它们，并赐予它们一片土地。

这片土地被分成N*M个格子，每个格子里写着’R’或者’F’，R代表这块土地被赐予了rainbow，F代表这块土地被赐予了freda。

现在freda要在这里卖萌。。。它要找一块矩形土地，要求这片土地都标着’F’并且面积最大。

但是rainbow和freda的OI水平都弱爆了，找不出这块土地，而蓝兔也想看freda卖萌（她显然是不会编程的……），所以它们决定，如果你找到的土地面积为S，它们将给你3*S两银子。

输入格式

第一行包括两个整数N,M，表示矩形土地有N行M列。

接下来N行，每行M个用空格隔开的字符’F’或’R’，描述了矩形土地。

每行末尾没有多余空格。

输出格式

输出一个整数，表示你能得到多少银子，即(3*最大’F’矩形土地面积)的值。

数据范围

1≤N,M≤1000

输入样例：

1
2
3
4
5
6
5 6
R F F F F F
F F F F F F
R R R F F F
F F F F F F
F F F F F F

输出样例：

45

思想：

类似于最大子阵和，进行行压缩，枚举每一行作为一维的进行计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1005;
int h[N][N], n, m;
int s[N], wid[N];
int work(int a[])		//传入时转化为一维问题
{ 
    int width, top = 0, ans = 0;
    a[m + 1] = 0;
    for(int i = 1; i <= m + 1; i ++ )
    {
        if(a[i] > a[s[top]])    wid[i] = 1, s[++ top] = i;
        else
        {
            width = 0;
            while(a[i] < a[s[top]])
            {
                width += wid[s[top]];
                ans = max(ans, a[s[top -- ]] * width); 
            } 
            wid[i] = width + 1, s[ ++ top] = i;
        }
    }
    return ans;
}
int main()
{
    cin >> n >> m;
    char c;
    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ )
        {
            scanf(" %c", &c);
            if(c == 'F')
                h[i][j] = h[i - 1][j] + 1;		//进行递推，如果有f则为上一行 + 1，否则为0
        }
    int res = 0;
    for(int i = 1; i <= n; i ++ )    res = max(res, work(h[i]));	
				//二维数组，传入一维地址进行简化
    cout << res * 3 << endl;
    return 0;
}
0%