最大连续子序列

HDU - 1231 (一维)

给定K个整数的序列{ N1, N2, …, NK }，其任意连续子序列可表示为{ Ni, Ni+1, …,
Nj }，其中 1 <= i <= j <= K。最大连续子序列是所有连续子序列中元素和最大的一个，
例如给定序列{ -2, 11, -4, 13, -5, -2 }，其最大连续子序列为{ 11, -4, 13 }，最大和
为20。
在今年的数据结构考卷中，要求编写程序得到最大和，现在增加一个要求，即还需要输出该
子序列的第一个和最后一个元素。

Input

测试输入包含若干测试用例，每个测试用例占2行，第1行给出正整数K( < 10000 )，
第2行给出K个整数，中间用空格分隔。当K为0时，输入结束，该用例不被处理。

Output

对每个测试用例，在1行里输出最大和、最大连续子序列的第一个和最后一个元
素，中间用空格分隔。如果最大连续子序列不唯一，则输出序号i和j最小的那个（如输入样例的第2、3组）。
若所有K个元素都是负数，则定义其最大和为0，输出整个序列的首尾元素。

Sample Input

6
-2 11 -4 13 -5 -2
10
-10 1 2 3 4 -5 -23 3 7 -21
6
5 -8 3 2 5 0
1
10
3
-1 -5 -2
3
-1 0 -2
0

Sample Output

Huge input, scanf is recommended.

思想

动态规划，dp[i]表示选i作为序列的结尾

状态转移:

1.首先选则i作为结尾则 a[i] 必选
2.如果dp[i - 1]的 sum 即(dp[i - 1].dat) < 0, 则不选前一段序列，单独以a[i]作为序列
方程： dp[i] = max(dp[i - 1] + a[i], a[i])
本题新增问题: 求出最优序列的左右区间下标
运用结构体数组

(由于题设要求最小的l，r下标，则当dp[i - 1] == 0 true时，要进行l，r的更新)
由于必选a[i], 则下标r必定赋值为 dp[i - 1].dat = i;
1.如果选择前一个序列，则l由dp[i - 1].l转移过来
2.如果不选择前一个序列，则l更新为当前下标 dp[i - 1].l = i

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e4 + 5;
struct node{
	int dat, l, r;		// 和值，序列左右区间 
}dp[N];
int a[N];
int main()
{
	int n, l, r;
	while(cin >> n && n)
	{
		dp[0].dat = 0;				// 边界情况处理 
		dp[0].l = 1;
		for(int i = 1; i <= n; i ++)		scanf("%d", &a[i]);
		for(int i = 1; i <= n; i ++)
		{ 
			dp[i].dat = a[i];	 //由于必选a[i]，则值刚开始必有a[i]右区间必为 i  
			dp[i].r = i; 
			if(dp[i - 1].dat >= 0)		//选前一个序列 
			{
				dp[i].dat += dp[i - 1].dat;		//值加上前一个 
				dp[i].l = dp[i - 1].l;		//l由前一个序列转移过来 
			}
			else
				dp[i].l = i;			//不选以自己下标作为 左区间 
		}
		node ans;
		ans.dat = -0x3f3f3f3f;				//遍历所有找出答案 
		for(int i = 1; i <= n; i ++)
			if(ans.dat < dp[i].dat)
			{
				ans = dp[i];
			}
		if(ans.dat < 0)				//答案为负，则说明全序列都为负，按题设要求输出，0 和 第一个 ，最后一个区间 
			printf("0 %d %d\n", a[1], a[n]);
		else
			printf("%d %d %d\n", ans.dat, a[ans.l], a[ans.r]);			//输出答案 
	}
	return 0;
}

最大子矩阵(二维)

给定一个边长为n * m的矩阵，求其中的子矩阵

样例

4 4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2

最大子阵为:

9 2
-4 1
-1 8

输出

思路一

暴力枚举 + 前缀和处理
时间复杂度: $O(n^4)$
1.先用二维前缀和处理从(0,0) 到(i, j)所构成的矩阵
2.每个子矩阵求法
如下图: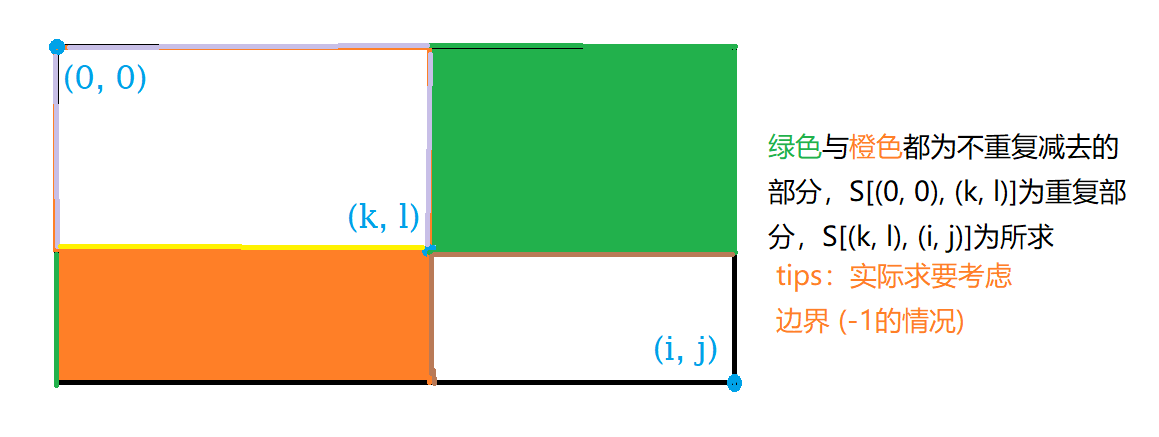

$$S[(k, l), (i, j)] = S[(0, 0), (i, j)] - S[(0, 0), (k - 1, j)] - S[(0, 0), (i, l - 1)] + S[(0, 0), (k - 1, l - 1)]$$

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 105;
int a[N][N];
int b[N][N];
int main()
{
    int n, m, ans = -1e8;
    cin >> n >> m;
 	for(int i = 0; i < n; i ++ )
        for(int j = 0; j < m; j ++ )
        {
            scanf("%d", &a[i][j]);
            b[i + 1][j + 1] = a[i][j] + b[i][j + 1] + b[i + 1][j] - b[i][j];  //下标从0开始对应 + 1
        }
	int sum = 0;
    for(int i = 0; i < n; i ++ )
        for(int j = 0; j < m; j ++ )
        {
            for(int k = 0; k <= i; k ++ )
                for(int l = 0; l <= j; l ++ )
                {
                    int sum = b[i + 1][j + 1] - b[k][j + 1] - b[i + 1][l] + b[k][l];
        			ans = max(ans, sum);
                }
        }
    cout << ans << endl;
    return 0;
}

思路二

动态规划 $O(n^3)$
把每一列压为一行，然后用二重循环枚举开头结尾(用前缀和快速求得每次压缩后的一维数组)
转化为一维数组问题后，d[i] = max(a[i] + d[i - 1], a[i]), 每次算出值后用更新ans

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 55;
int a[N][N];
int b[N][N];
int main()
{
    int n, m, ans = -1e8;
    cin >> n >> m;
 	for(int i = 0; i < n; i ++ )
        for(int j = 0; j < m; j ++ )
        {
            scanf("%d", &a[i][j]);
            b[i + 1][j + 1] = b[i][j + 1] + a[i][j];	//列方向前缀和
        }
    for(int i = 0; i < n; i ++ )		//二重枚举列方向压缩的起点和终点
        for(int j = i; j < n; j ++ )
        {
            int sum = 0;
            for(int k = 0; k < m; k ++ )	//一维问题
            {
                sum += b[j + 1][k + 1] - b[i][k + 1];	
                ans = max(ans, sum);
                if(sum < 0)	sum = 0;			//小于零则前段扔掉
            }
        }
    cout << ans << endl;
    return 0;
}